Why Sample-Based Planning

Why Sample-Based Planning?

So why exactly can’t we use discrete planning for higher dimensional problems? Well, it’s incredibly hard to discretize such a large space. The complexity of the path planning problem increases exponentially with the number of dimensions in the C-space.

Increased Dimensionality

For a 2-dimensional 8-connected space, every node has 8 successors (8-connected means that from every cell you can move laterally or diagonally). Imagine a 3-dimensional 8-connected space, how many successors would every node have? 26. As the dimension of the C-space grows, the number of successors that every cell has increases substantially. In fact, for an n-dimensional space, it is equal to 3^n - 1 .

It is not uncommon for robots and robotic systems to have large numbers of dimensions. Recall the robotic arm that you worked with in the pick-and-place project - that was a 6-DOF arm. If multiple 6-DOF arms work in a common space, the computation required to perform path planning to avoid collisions increases substantially. Then, think about the complexity of planning for humanoid robots such as the one depicted below. Such problems may take intolerably long to solve using the combinatorial approach.

Constrained Dynamics

Aside from robots with many degrees of freedom and multi-robot systems, another computational difficulty involves working with robots that have constrained dynamics. For instance, a car is limited in its motion - it can move forward and backward, and it can turn with a limited turning radius - as you can see in the image below.

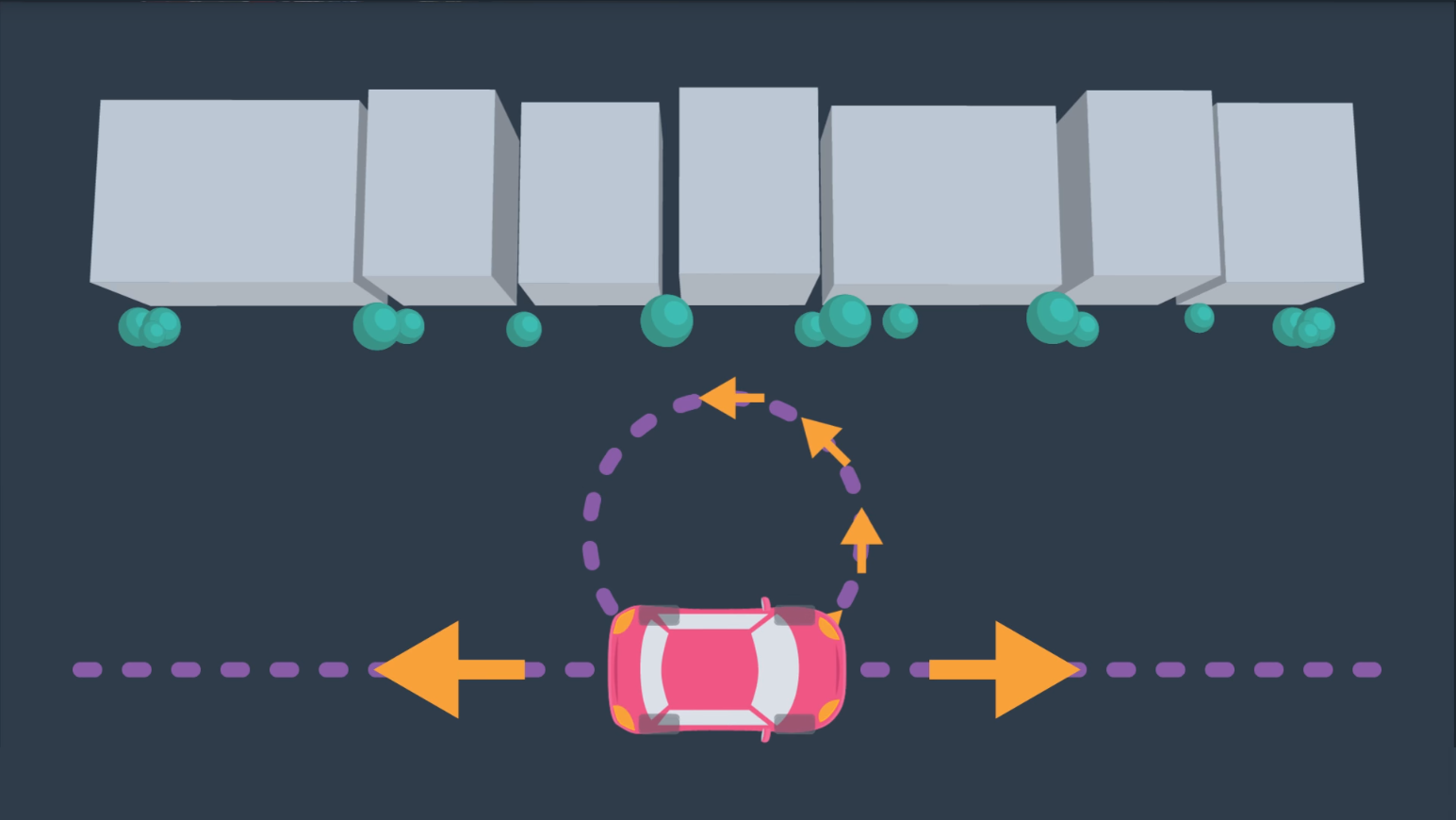
However, the car is not able to move laterally - as depicted in the following image. (As unfortunate as it is for those of us that struggle to parallel park!)

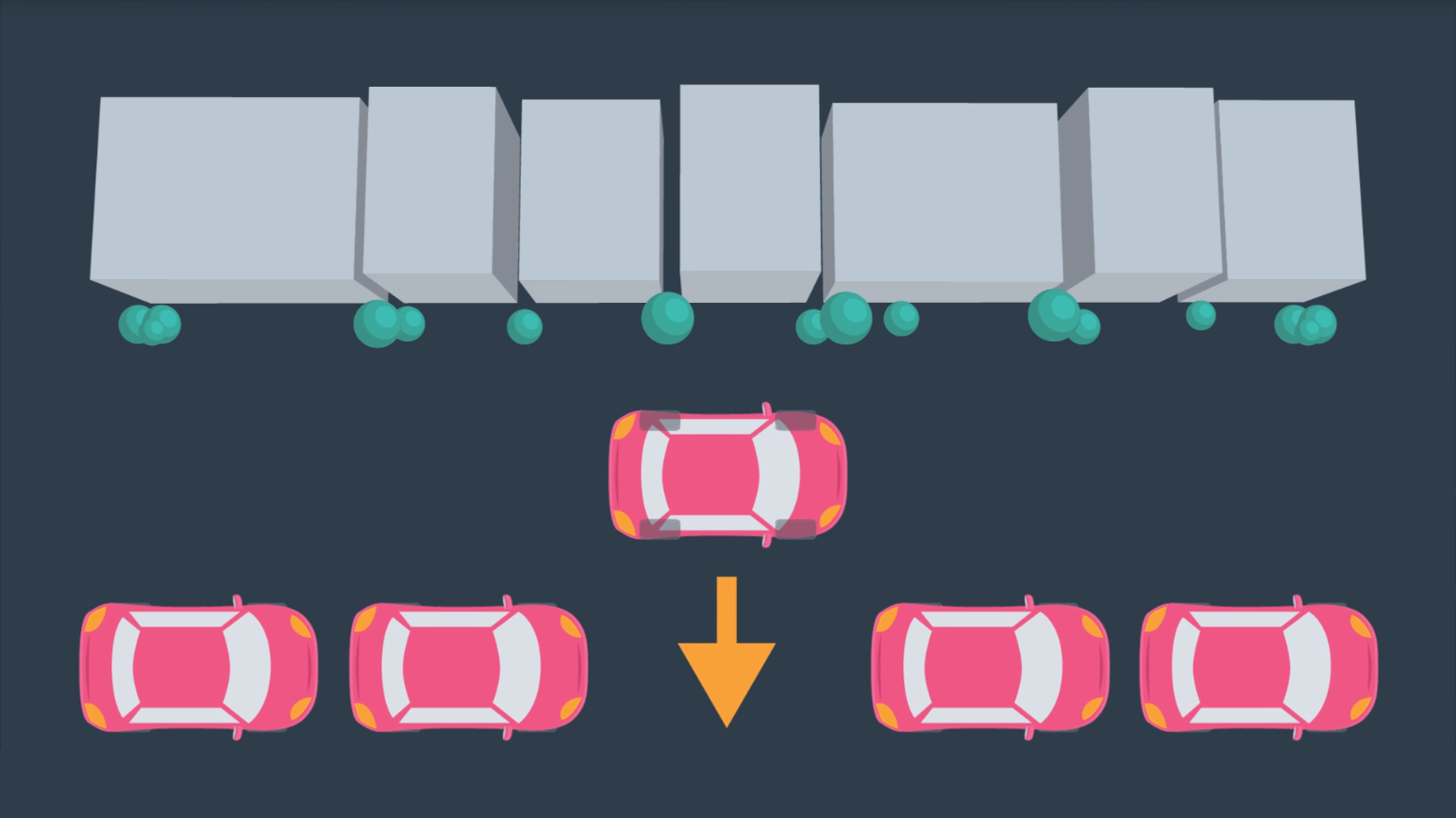
In the case of the car, more complex motion dynamics must be considered when path planning - including the derivatives of the state variables such as velocity. For example, a car's safe turning radius is dependent on it's velocity.

Robotic systems can be classified into two different categories - holonomic and non-holonomic. Holonomic systems can be defined as systems where every constraint depends exclusively on the current pose and time, and not on any derivatives with respect to time. Nonholonomic systems , on the other hand, are dependent on derivatives. Path planning for nonholonomic systems is more difficult due to the added constraints.

In this section, you will learn two different path planning algorithms, and understand how to tune their parameters for varying applications.